Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 5397번
- graphical models
- 자바ORM표준JPA프로그래밍
- 이것이 MySQL이다
- 개발순서
- Fisher discriminant analysis
- chapter02
- 인공지능
- CH01
- 알고리즘
- 델타 rule
- 스터디
- undirected graphical model
- falsePosition
- bisection
- 1차예선
- 선형분류
- 선형판별분석
- 로지스틱 회귀
- MySQL
- directed graphical model
- 근구하기
- Perceptron Convergence theorem
- 2018
- chapter01
- secant
- vector미분
- Numerical optimization
- SCPC
- 알고리즘대회
Archives
- Today
- Total
computer_study
[수치해석] 근 구하기 예제 본문
문제 내용
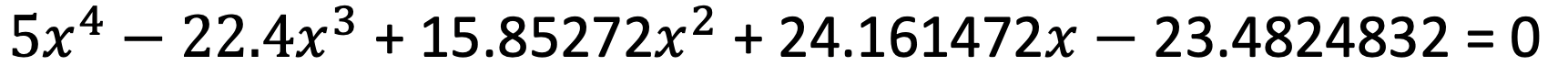
해결 과정
해당 방정식은 4차 방정식이기에, 몇가지 수를 넣어보고 대략적으로 다음과 같은 그림을 얻을 수 있었다.
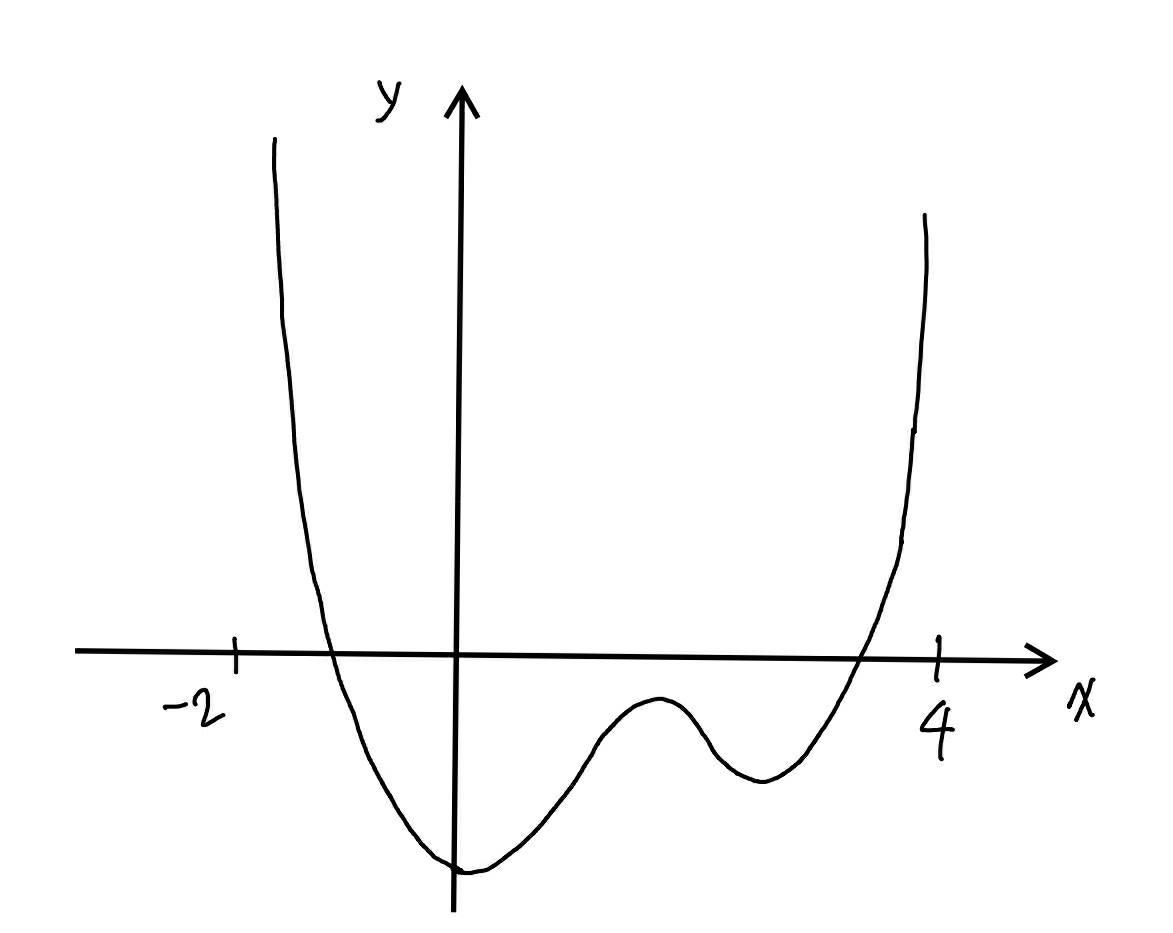
이후 Bisection과 Newton-Raphson방식을 사용하여 문제를 해결하였다.
bisection
- 그래프의 모양을 참고하여, 넉넉히 ( -4 ~ 9 ) 구간을 1씩 나누어 진행하였다.
- Epsilon은 0.001로 stop condition을 잡아 오차범위를 설정하였다 .
- Interval 양 끝 각각의, 함수 값의 곱이 음수일 때, bisection을 이용하여 interval을 줄여주었다.
- 결과는 두개의 값 (-1.04395, 3.12402)이 나왔다.
1. 주어진 함수 구현
double f(double x){
return 5*pow(x,4) -22.4*pow(x,3) +15.85272*pow(x,2) +24.161472*x -23.4824832;
}2. bisection 구현
int interval = 1;
int tmp= -4;
int interval_start = interval * tmp;
while(interval_start < 10){
interval_start = interval * tmp;
double interval_min = interval_start;
double interval_max = interval_start + 1;
double xr = 99999;
while(interval_max - interval_min > Epsilon){
if(f(interval_min)*f(interval_max) >0)
break;
xr = (interval_min + interval_max) / 2;
if(f(xr) == 0)
break;
else if(f(interval_min) * f(xr) <0 )
interval_max = xr;
else
interval_min = xr;
}
if(xr != 99999)
bisection_result.push_back(xr);
tmp++;
}
bisection 장단점
- 장점 : 구간 양쪽의 함수 값을 비교하여 근의 존재 여부를 판단한다는 개념 자체가 직관적이어서 쉽게 구현할 수 있었다.
- 단점 : 중간에 중근이 존재 할 가능성이 있으나, 이 방법으론 중근의 존재를 알 수 없었다.
Newton-Raphson
- Newton_raphson함수에서 Initial x값을 입력 값으로 받아, Epsilon 범위에 들어올 때 까지 다음 x를 찾는 과정을 반복한다.
- 현재 x값과 다음 x값의 차이가 Epsilon보다 작다면 (수렴했다면) 그 값을 반환해준다.
- 그래프를 참고하면, 양쪽에 근이 하나씩 존재하므로 initial 값으로 근과 가까운 -2와 4를 넣어주었다.
- 1,2,3 사이에 근이 존재 할 가능성이 있기 때문에 initial값으로 1,2,3을 넣어주었다.
- 결과는 (-1.04422, 1.19843, 1.20106, 3.12477, 3.12425) 가 나왔고 이로 미루어보아 이 방정식은 근으로 -1.04, 3.12 와 중근 1.20을 가지는 것을 알 수 있다.
1. 주어진 함수에 대한 미분 값을 반환하는 함수
double f_prime(double x){
return 20*pow(x,3) -22.4*3*pow(x,2) +15.85272*2*x +24.161472;
}2. newton_raphson함수
double newton_raphson(double x){
double delta_x = f(x)/f_prime(x);
while(abs(delta_x) >= Epsilon){
x = x - delta_x;
delta_x = f(x)/f_prime(x);
}
return x;
}3. 여러 Initial값 대입
newton_result.push_back(newton_raphson(-2));
newton_result.push_back(newton_raphson(1));
newton_result.push_back(newton_raphson(2));
newton_result.push_back(newton_raphson(3));
newton_result.push_back(newton_raphson(4));
Newton-raphson 장단점
- 장점 : - 근을 찾기 위한 다음 xr값을 하나의 step에 구할 수 있기에 구현이 편리했다.
- 일반 근 뿐만 아니라 중근까지 구해낼 수 있었다. - 단점 : 그래프를 보고, 적절한 initial값을 주지 않는다면 근을 찾기가 불가능할 수 있다. 또한 몇몇 그래프들은 수렴하지 않기 때문에 근을 찾기 불가능하다.
전체 코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#define Epsilon 0.001
using namespace std;
double f(double x){
return 5*pow(x,4) -22.4*pow(x,3) +15.85272*pow(x,2) +24.161472*x -23.4824832;
}
double f_prime(double x){
return 20*pow(x,3) -22.4*3*pow(x,2) +15.85272*2*x +24.161472;
}
double newton_raphson(double x){
double delta_x = f(x)/f_prime(x);
while(abs(delta_x) >= Epsilon){
x = x - delta_x;
delta_x = f(x)/f_prime(x);
}
return x;
}
int main(){
vector<double> bisection_result;
vector<double> newton_result;
int interval = 1;
int tmp= -4;
int interval_start = interval * tmp;
while(interval_start < 10){
interval_start = interval * tmp;
double interval_min = interval_start;
double interval_max = interval_start + 1;
double xr = 99999;
while(interval_max - interval_min > Epsilon){
if(f(interval_min)*f(interval_max) >0)
break;
xr = (interval_min + interval_max) / 2;
if(f(xr) == 0)
break;
else if(f(interval_min) * f(xr) <0 )
interval_max = xr;
else
interval_min = xr;
}
if(xr != 99999)
bisection_result.push_back(xr);
tmp++;
}
newton_result.push_back(newton_raphson(-2));
newton_result.push_back(newton_raphson(1));
newton_result.push_back(newton_raphson(2));
newton_result.push_back(newton_raphson(3));
newton_result.push_back(newton_raphson(4));
cout << "Bisection: ";
for(int i=0 ; i< bisection_result.size() ; i++){
cout << bisection_result[i] <<" ";
}
cout << endl;
cout << "Newton-raphson: ";
for(int i=0 ; i< newton_result.size() ; i++){
cout << newton_result[i] <<" ";
}
cout << endl;
return 0;
}'학교수업정리 > 수치해석' 카테고리의 다른 글
| [수치해석] 02. Finding Min/Max (0) | 2020.09.13 |
|---|---|
| [수치해석] 01. Finding Roots (0) | 2020.09.04 |
Comments


