| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- MySQL
- graphical models
- vector미분
- 알고리즘대회
- 5397번
- 선형분류
- falsePosition
- Perceptron Convergence theorem
- CH01
- Numerical optimization
- chapter02
- bisection
- chapter01
- 스터디
- 2018
- 자바ORM표준JPA프로그래밍
- secant
- 델타 rule
- 로지스틱 회귀
- 선형판별분석
- 알고리즘
- 이것이 MySQL이다
- 인공지능
- 근구하기
- 1차예선
- SCPC
- directed graphical model
- 개발순서
- Fisher discriminant analysis
- undirected graphical model
- Today
- Total
computer_study
[수치해석] 02. Finding Min/Max 본문
수치해석에서의 Min/Max 구하기
min/max 값을 구할 땐, 보통 그 min 값이나 max값이 주 목적이 된다. (ex. 돌을 하늘로 던졌을 때, 최대로 높이 올라간 높이는?)
수치해석에서 min/max구하는 문제는 변수(parameter)를 최적화하는 문제이다.
cost나 energy값 자체보단, 그 값들이 min/max값을 갖게 하는 변수가 중요하고 이 변수가 실질적인 solution이다.
앞선 01.Root에선 f(x)=0이 되는 x값을 구하는 문제였다면 Min/Max찾기는 f '(x)=0이 되는 x값을 찾는 것이다.
과정은 비슷하지만, f ''(x) (이계도함수)가 사용된다.

Global과 Local
global min/max는 모든 구간에서 min/max인 값을 얘기하고
local min/max는 주변보다 min인 값 혹은 주변보다 max값을 얘기한다.
실제 global min/max를 찾는 것이 가장 이상적이지만 이는 매우 어려운 일이다.(보통 local을 구하게 되거나 global인지 local인지 구별할 수 없다.)
최대한 global값을 찾기 위해선 다음과 같은 과정들을 시도해야된다.
- 함수를 non-negative 함수로 만들기 위해서(min/max찾기 좋다) 제곱의 꼴을 띄고있는 함수로 만들어준다.
- 시작점을 random하게 바꿔가며 min/max값을 찾아본다.
- 위 두 방법을 사용하며 최적의 값을 찾아낸다.
Golden-Section Search
한 interval안에 min이나 max를 하나만 가지고 있다고 가정하여 값을 찾는다.
golden-section은 황금비율에 따라 interval을 나누어준다. (ratio= 1.6180...)
장점
- 세분화된 간격에서 min/max를 보장한다.
- 1차미분 같은 연산이 필요없다.(연산을 덜 수행하는 알고리즘)
- 절반씩 나누지 않기 때문에 수렴 속도가 bisection보다 빠르다. (cf. bisection은 ratio= 2.0 & 1차미분 필요)
golden-ratio란?

l1과 l2의 위치를 바꿔서 생긴 보조선은 l1을 또다시 황금비율로 나눈다.

Golden-ratio 이용한 search
위 그림을 보면, x1부터 l1을 시작할지, xu부터 l1을 시작할지 알 수 없다. Golden-section search는 이를 반복적인 알고리즘을 통해서 정하고, interval을 줄여나간다.
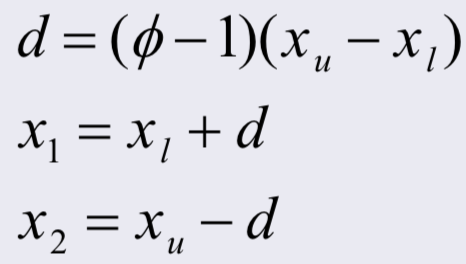
황금비율 중 긴 쪽의 길이를 d로 잡고, xl은 interval의 lower bound, xu 는 interval의 upper bound를 나타낸다. 이 때, x1과 x2는 다음과 같이 잡는다.

d가 xl에서 시작할지 xu에서 시작할지 모르기에 x1과 x2에서의 함수값을 비교하여 interval을 다시 지정해준다.
- f(x1) < f(x2)라면 x2가 새로운 lower bound (xl)가 되고 x1이 새로 만들어진 interval의 x2값이 된다. (x1값만 새로 구해주면 된다.)
- f(x1) > f(x2)라면 x1이 새로운 upper bound (xu)가 되고 x2가 새로 만들어진 interval의 x1값이 된다. (x2값만 새로 구해주면 된다.)
xl 혹은 xu 둘 중 하나는 이전 단계에서 구하기 때문에, 계산량을 줄일 수 있다.
example

다음과 같은 모양을 가진 식이 주어졌을 때, golden-section search를 이용해 min값을 같게 하는 x를 구하는 과정은 다음과 같다.

Parabolic Interpolation
2차함수를 사용하여 최적의 값을 찾는 방법이다.
3개의 점을 알고있으면, 그에 해당하는 2차함수를 fitting할 수 있고, 그 2차함수의 min/max값을 갖는 x를 다음 x로 정한다.
최근 3개의 점으로 2차함수를 계속 fitting해가며 실제 함수의 min혹은 max값을 찾는다.
x1,x2,x3를 알 때, 다음 x (x4)를 찾는 방법

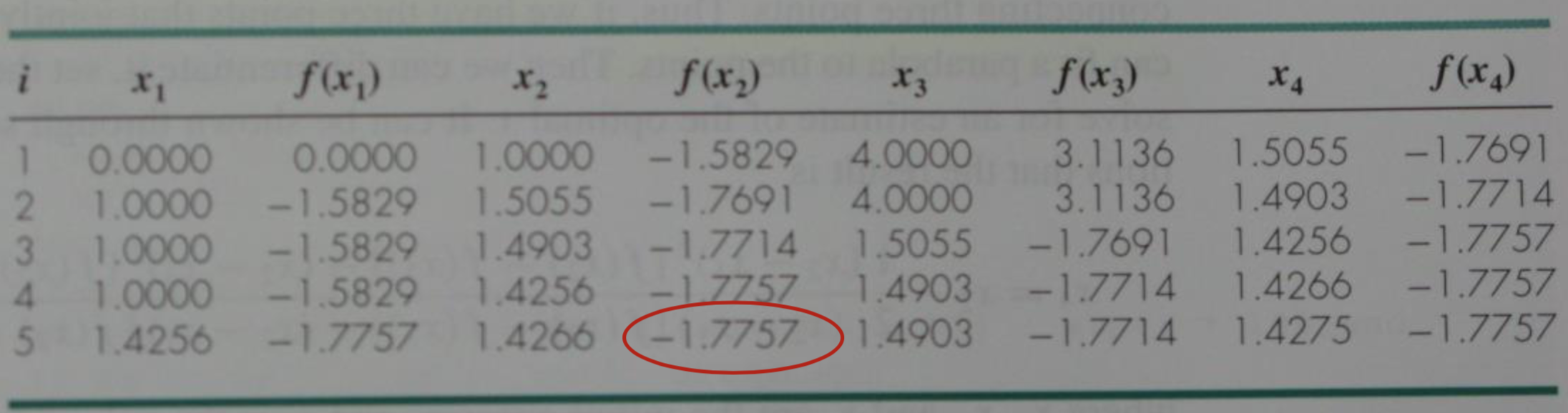
위 example을 parabolic interpolation을 사용하여 해결하는 과정
Gradient Descent Method
기울기가 있는 쪽으로 점점 감소시켜가며 최소값을 찾을 수 있다.

이 방법은 얼만큼을 이동해주어야 되는지 명확하지 않아, 알파값을 실험적으로 정해주어야 된다.
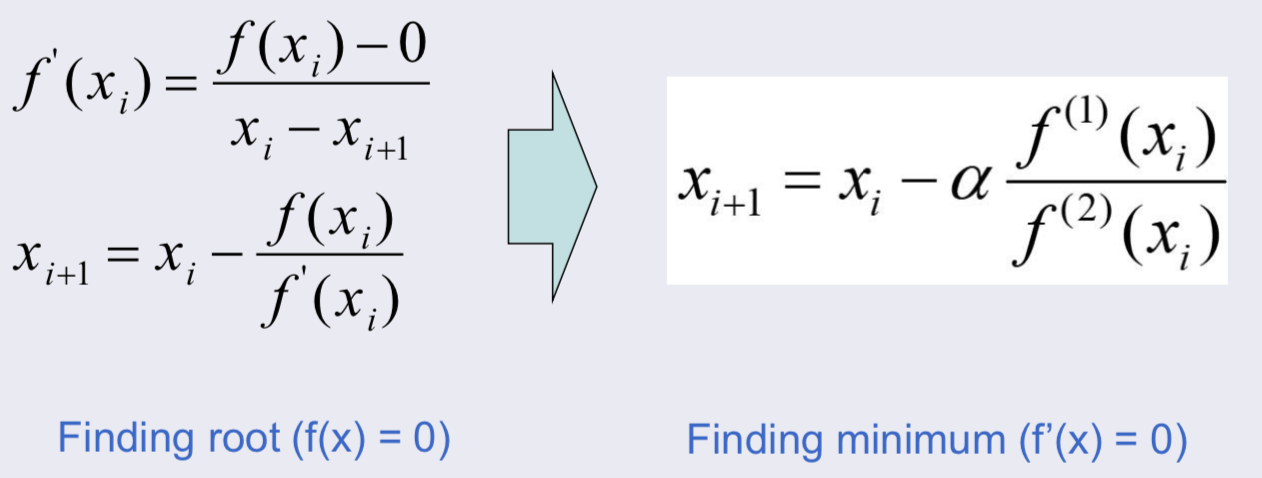
Newton Method
root를 찾을 때 했던 방식을 사용하며, f(x), f'(x) 대신 f'(x), f''(x)를 사용한다.
증명
- 테일러 급수에 의해
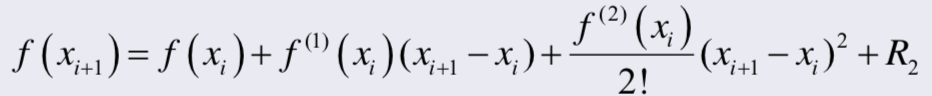
2. 2차함수로 approximation이 된다면 3차항 4차항은 필요가 없으므로 R2는 의미가 없고 사실 상 0에 가깝다. (R2 생략)
3. min이거나 max라는 의미는, x에 변화에 따라 함수값의 변화가 거의 없다는 것이다.

4. 2,3번을 이용하여 1번 식을 정리하면 다음과 같은 식이 나온다.
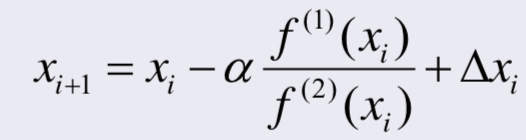
△xi는 모멘트 값으로, 일정 값을 x값에 더해주어 수렴 속도는 느려질 수 있으나 안정적으로 수렴할 수 있도록 한다. (진동시에는 더 빨리 수렴할 수 있다.)
다음 x값이 f'(xi)/f''(xi)에 의해 변동하기 때문에, 미분값들에 영향을 많이 받는다.

이계도함수를 구하는 방법
미분을 통해 이계도함수를 구하기 어려울 때에는 approximation하여 구해줄 수 있다.

위와 같은 그래프가 있을 때 이계도함수는 h가 매우 작은 수일 때
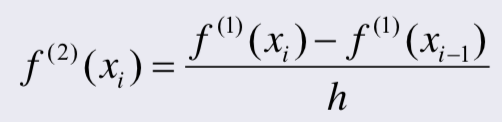
이다. 이때, f'(xi) 와 f'(xi-1)은 각각 다음과 같다.

위 두 식을 처음 식에 대입하면 f의 이계도함수는 다음과 같이 얻을 수 있다.
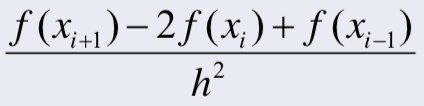
Multi-dimension
variable이 두개 이상일 때를 말한다. (ex. f(x,y))
- 각 variable 방향으로 변화율을 구하기 위해 Gradient vector가 필요하다.(각 요소마다 미분을 더해준 vector)
- 함수가 각 variable방향으로 존재하기 때문에, Jacobian이 필요하다.
- 두번 미분 한 값을 구하기 위해 Hessian matrix가 필요하다.
이는 Newton Method를 vector모양의 n차원 공간으로 확장하여 구할 수 있다.

Expansion of Newton Method
newton method는 neural network나 deep learning optimization에 사용될 수 있다.
multi-layer perceptron model의 경우, weight같은 구해줘야 될 parameter들이 newton method를 근간으로 update되고, 수렴한 값을 만들어준다.

perceptron algorithm(퍼셉트론 알고리즘)
- 학습하려하는 대상들의 결과를(원하는 출력값) 설정한다.
- weight를 random하게 혹은 uniform하게 초기화한다.
- 각각 input에 대해 output들을 계산한다.
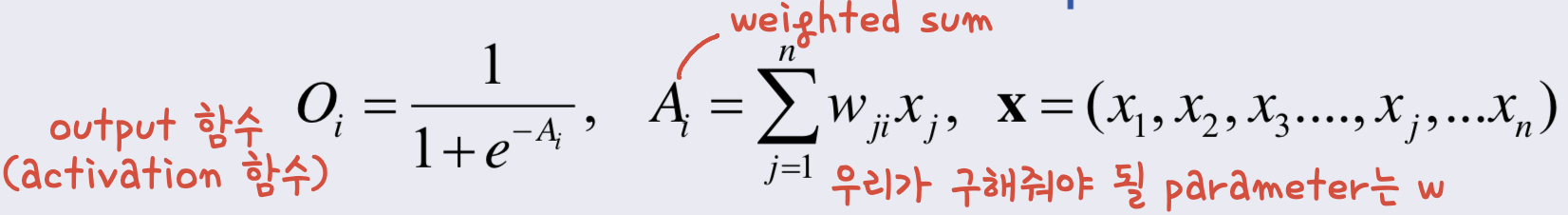
- 전체 energy를 계산해준다.(이 값이 min이 되는 w를 찾아 update해주면 된다.)
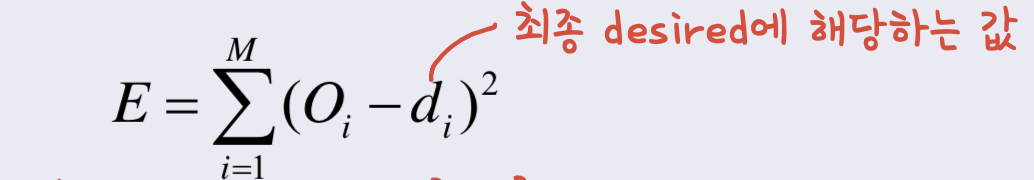
- gradient descent를 따르며 weight를 update해준다.(식의 골격은 newton method를 따른다.)

식의 뒤에 △w를 추가하여 moment term을 넣을 수도 있다.
'학교수업정리 > 수치해석' 카테고리의 다른 글
| [수치해석] 근 구하기 예제 (0) | 2020.09.06 |
|---|---|
| [수치해석] 01. Finding Roots (0) | 2020.09.04 |


