| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 알고리즘
- 선형분류
- 알고리즘대회
- Numerical optimization
- 근구하기
- MySQL
- chapter02
- Fisher discriminant analysis
- CH01
- 2018
- graphical models
- 5397번
- 인공지능
- 1차예선
- 개발순서
- 로지스틱 회귀
- falsePosition
- 선형판별분석
- 이것이 MySQL이다
- directed graphical model
- Perceptron Convergence theorem
- 스터디
- chapter01
- vector미분
- SCPC
- 자바ORM표준JPA프로그래밍
- 델타 rule
- bisection
- undirected graphical model
- secant
- Today
- Total
computer_study
[인공지능] cover's theorem, Kernel methods 본문
용어정리
Linear classifier
Linear classifier은 앞성 작성 한 내용들 처럼 Logistic regression, Fisher discriminant analysis, Large margin classifier이 있다.
이들은 선을 통해서 데이터를 분류하는 방법을 말한다.
이러한 Linear classifier은 dimension에 영향을 받는다. dimension이 D, data 수가 N이라고 할 때, D >= N-1 이면 label이 어떤 식으로 존재하던 linear classifier하다고 할 수 있다.(아래 covers theorem에서 증명) 예를 들어, 데이터가 1개 ~ 4개라면, 3차원 공간에서 이들을 완벽하게 classifier하는 hyper plane을 만들 수 있다는 것이다.
Dichotomy (이분법)
- 데이터를 두 개의 set으로 나누는 행위를 말한다.
- N개의 데이터가 있을 때, 데이터가 두개의 set 중 하나이기 때문에 총 가능한 경우의 수는 2N 개라고 할 수 있다.
- D dimensional space가 있으면, 위 Linear classifier에서 언급한 것 처럼 N=D+1개라면 모든 데이터를 완벽하게 classify할 수 있고, 2D+1의 다른 dichotomy에 대해 분류할 수 있는 power를 가진다.
Cover's theorem
linear classifier을 얼만큼 잘 하는가를 표현 해주는 방법이다.
- 표기법 : c(n, d)
- 의 미 : n개의 data, d개의 dimensional space가 있을 때 linearly separable한 dichotomies의 개수를 말한다.

새로운 데이터가 추가될 때, 하나의 class에 들어갈 수 밖에 없는 경우는 non-ambiguous (모호하지 않다) 라고 한다.
새로운 데이터가 추가될 때, 어느 class에도 들어갈 수 있는 경우는 데이터가 ambiguous(모호하다) 라고 한다.
새로운 데이터가 추가된다면 이 두 경우 중 하나가 되고, ambiguous한 경우엔 dichotomies가 추가되게 된다. (여러 class로 분류될 수 있기 때문에)
따라서 c(n,d)라는 linearly separable한 데이터에 새로운 data가 추가된다면
c(n+1, d) = c(n, d) + c(n, d-1) 이 된다.
( c(n,d) 는 현재까지의 class로 분류되는 경우 , c(n, d-1)은 추가로 더해지는 dichotomy의 개수)
* 추가로 더해지는 dichotomy의 개수가 c(n, d-1)이 되는 이유
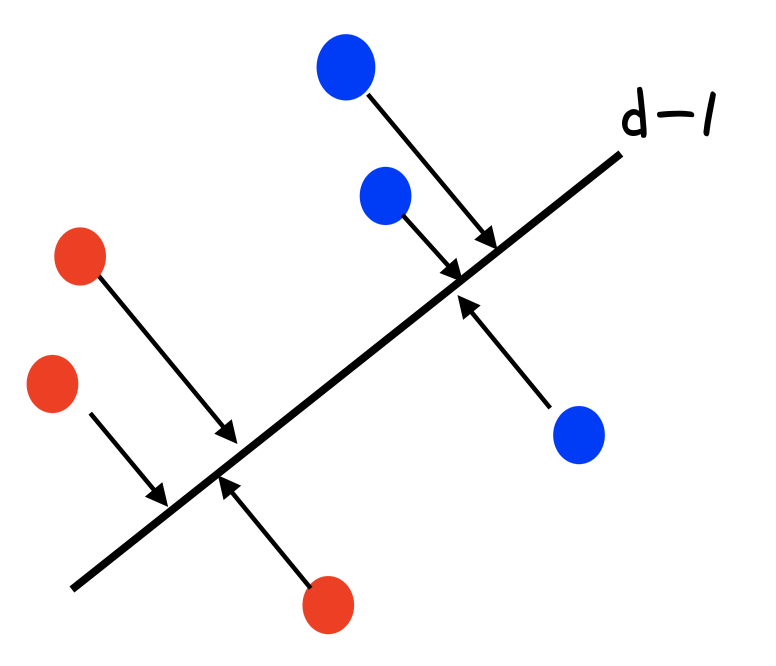
위 그림과 같이 n개의 데이터를 d-1 dimension에 projection 했을 때 separable 하다면 ambiguous한 데이터를 무조건 추가할 수 있으므로 새로운 n+1번째 데이터가 ambiguous 하게 만드는 pattern의 개수는 c(n, d-1)이 된다.
c(n,d)를 recursive하게 표현 가능하므로 이를 그림으로 그려보면 다음과 같다.

위와같은 그림을 식으로 정리해보면 다음과 같이 표현 가능하다.

이를 토대로, n개의 data를 d- dimensional space에 뿌린 후 label을 random으로 잡을 때 data가 linearly separable 할 확률을 구하면

이때, n-1보다 d가 크거나 같다면 확률이 1이 나오기 때문에, 무조건 linearly separable해진다.
* cover's theorem의 특징
d가 n-1보다 크면 무조건 linearly separable해지고, flexible하긴 하지만 dimensionality가 커질수록 잘못된 데이터(노이즈)에 대해서도 학습하는 overfitting이 발생한다.
반대로 dimensionality가 작아진다면, overfitting은 일어나지 않지만 flexible하지 않고, 모두가 잘 학습이 되지 않는 확률을 가지게 된다.
새로운 데이터가 abiguous 할 확률
d dimensional space에서 (n+1)번째 데이터가 ambiguous할 확률을 A(n,d)라고 한다면

예를들어, A(10,3) 이라면 c(10,2)/c(10,3)이 되고, 그 값이 23/65이 된다.

이는 11번째 데이터가 들어왔을 때 ambiguous 할 확률이 23/65이 된다는 의미이다. 일반적인 그래프로 그려보자면

다음과 같은 모양이 되는데, 데이터의 수가 dimension에 2배가 될 때 까지는 데이터를 계속 넣어도 그 데이터를 학습해서 fitting이 가능하다는 의미이다. 다만 그 이후가 되면, 떨어지는 확률 만큼만 새로운 데이터를 학습할 수 있다는 의미이다.
data가 N개까지 linearly separable 하고, N+1부터 non-separable해지는 경우.

정리하자면, n<=d+1일 때 까지는 항상 separable 하고, 그 이후부터는 pr(n)의 확률을 가지고 linearly separable을 하다는 얘기가 된다.
이때 E[n] = 2d가 되고, Median[n] = 2d가 된다. (E[n]의 의미는 처음 linearly separable이 깨지는 지점의 expectation)

d+1 지점이 지나서도 linearly separable 할 확률이 높고 그 기대값이 2d이다
바꿔말하면, n이 고정되어있고 d가 증가하는 상황으로 볼 수도 있다.
d<=n-1일 때 가지는 p_r(n)의 확률을 가지고 linearly separable하고 n-1부터는 항상 separable하다고 할 수 있다.

Kernel method (kernel trick)
데이터를 linear classifier하게 분류하려할 때, 절대로 분류할 수 없는 경우가 존재한다.

이런 데이터를 linear separable하게 분류되지 않을 때, dimension을 높여줌으로써 해결할 수 있다.
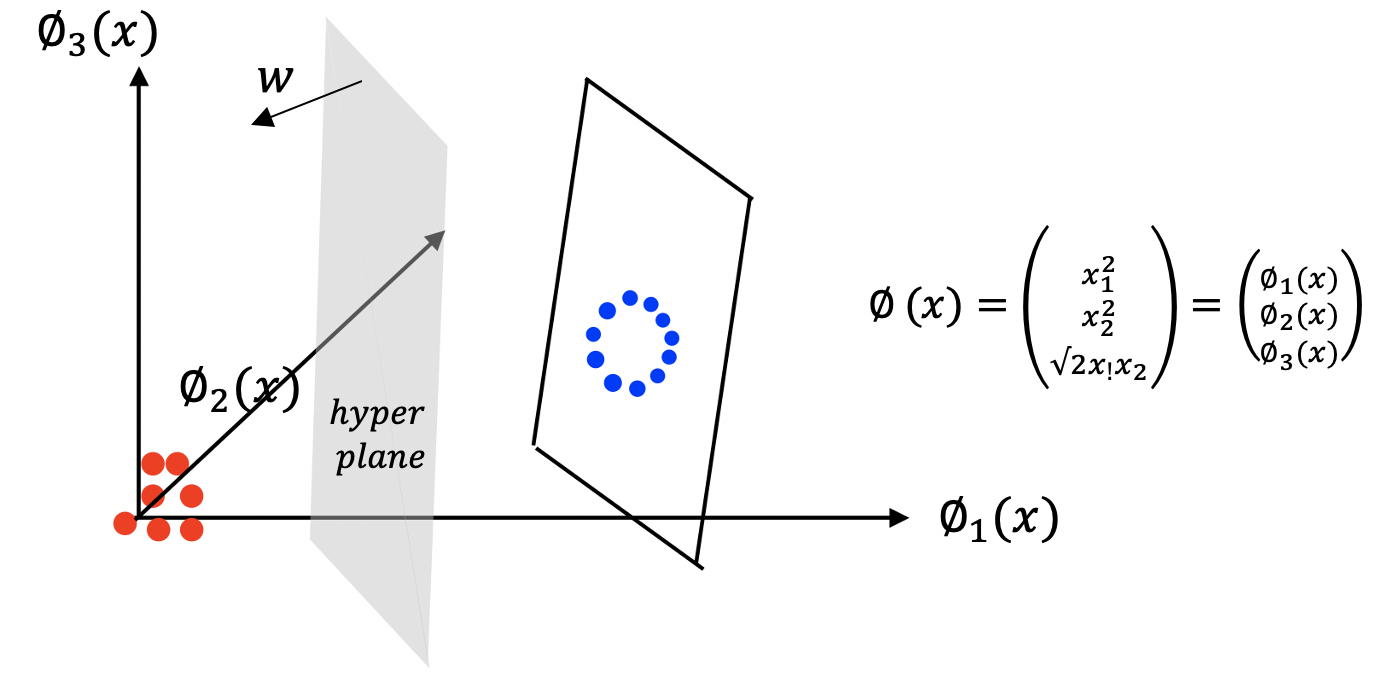
파이 함수를 임의로 잡아 2차원 공간의 데이터들을 3차원으로 mapping시키면 데이터가 linear separable해진다.
이렇게 mapping한 데이터들을 SVM(supporting vector machine)을 이용하여 분류한다고 해보자.
SVM의 dualform은 다음과 같다. (SVM에 대한 정리 knowable.tistory.com/46)

위 식 중 x에 mapping함수를 적용한다면 xi, xk대신 파이 함수가 들어가게 되고, 그를 inner product하는 과정이 포함되게 된다.
이러한 과정을 순서대로 수행한다면 아래 식과 같이 1. 파이라는 함수를 이용하여 차원을 바꾼 후, 2. 두 식을 inner product해주어야 된다.

이렇게 두 단계로 진행해야 되는 과정을 하나로 줄여서 사용 가능하게 한다는 것이 kernel method이다.
SVM에서 class를 판별해주는 판별식에도 kernel method를 적용할 수 있다.


kernel method에 쓰이는 대표적인 kernel함수들은 다음과 같다.

example (polynomial kernel)

Mercer's theorem
kernel 함수가 positive definite 한 함수라면, 파이함수를 굳이 따져 볼 필요 없이, 위 조건들을 만족하는 kernel 함수가 존재한다는 이론이다.
'학교수업정리 > 인공지능' 카테고리의 다른 글
| [인공지능] Graphical models (0) | 2020.11.30 |
|---|---|
| [인공지능] probability model and parameter estimation (0) | 2020.11.27 |
| [인공지능] Optimization with constraint, Large margin methods (0) | 2020.10.14 |
| [인공지능] Nearest neighbor methods(이웃 알고리즘), KNN (2) | 2020.10.09 |
| [인공지능] Perceptron Convergence theorem (0) | 2020.10.06 |




