| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 로지스틱 회귀
- MySQL
- 2018
- chapter01
- 5397번
- falsePosition
- CH01
- Numerical optimization
- graphical models
- 스터디
- 알고리즘대회
- 선형분류
- 알고리즘
- 자바ORM표준JPA프로그래밍
- 1차예선
- 개발순서
- undirected graphical model
- 선형판별분석
- bisection
- 델타 rule
- Perceptron Convergence theorem
- secant
- SCPC
- chapter02
- directed graphical model
- 이것이 MySQL이다
- 근구하기
- Fisher discriminant analysis
- vector미분
- 인공지능
- Today
- Total
computer_study
[인공지능] probability model and parameter estimation 본문
Gaussian probability density function
일반적인 가우시안 분포

d차원 space 상에서 정의된 가우시안 (multivariate gaussian)
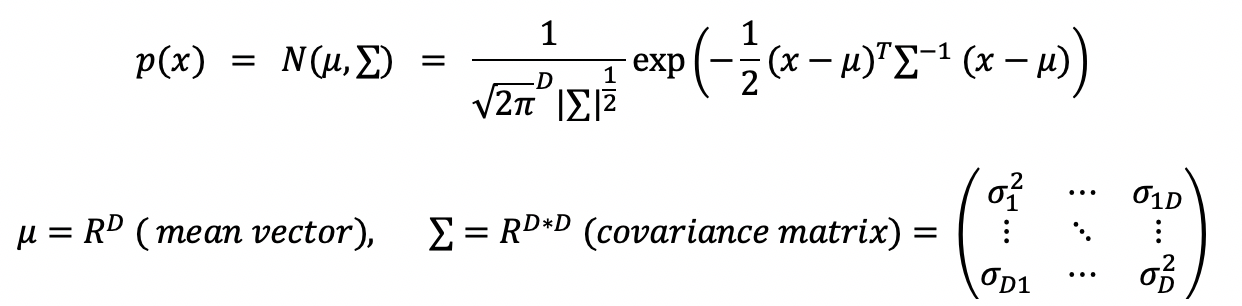
위 식에서 p(x) = p(x1, x2...xD ) 즉, marginal pdf이기 때문에, x = (...x1 ... x2 ...xD...) 를 뜻한다.
시그마는 DxD covariance matrix로, symmetric positive definite matrix이다. (∑ = ∑T , 6ij = 6ji)
그림으로 vocariance matrix를 보자면 다음과 같다.

d차원 space 상에서 정의된 가우시안을 임의의 direction(w) 에 projection

conditional probability density function
joint probability p(x1,x2)로 부터 conditional probability p(x1|x2)알아내기.
d차원 space 상에서 정의된 가우시안 에서, ∑의 요소들을 a11 ~ add 로 생각하고, exp 안쪽 계수를 2차방정식의 완전제곱 꼴로 바꾸어서 또 다른 가우시안 형태를 만들어낼 수 있다.
우선 위 multivariate gaussian의 식을 이용해서 p(x1, x2)를 우선적으로 구해보면

위식을 이용하여 conditoinal probability를 구할 수 있는데, 증명을 생략하고 결과만 정리하면

original multivariate gaussian 에서 p(x1|x2) 꼴을 얻어낼 수 있다.

marginal probability pensity function
joint probability p(x1,x2)로 부터 marginal probability p(x1)알아내기
p(x1,x2)로 부터, p(x1)을 구하기 위해선 p(x1, x2)를 x2로 적분하여야 된다.


이렇게 p(x1)은 x1에 대한 가우시안이 된다. 즉, original parameter에서 x1을 제외한 나머지 parameter가 원래 없었던 것 처럼 빠져버리게 된다.
데이터로부터 학습하는 방법(learning)
데이터가, D dimension에 속하는 x 값들이 있고, 그 x들마다 y값이 존재한다고 하자. ( x1,x2,...xN∈RD , y1,y2,...yN∈R )
jointly gaussian을 생각하기 위해 새로운 variable z = ( ~~x~~ y) ∈ RD+1 이라 하고 우리의 모델을 p(z) = N(μz, ∑z)로 잡는다
이때, 데이터를 이용해서 N(μz, ∑z)을 구해내는 것이 학습이다. (가우시안의 mean, variance를 데이터로부터 얻어낼 수 있다.)
데이터를 이용해 가우시안 form을 올바르게 generation시킬 확률이 가장 큰 μz, ∑z 를 구해야 되므로


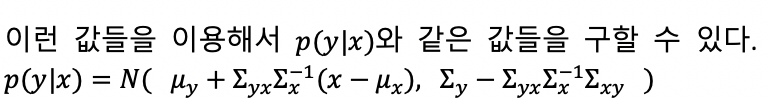
즉, 데이터 중 몇개의 숫자가 없어도 optimal한 μ를 찾는것이 가능하다.
예를들어, z = (x1, x2, y)로 이루어져있는데, x2를 모른다면, p(x1,x2,y) -> p(x1,y)로 변환 후
p(y | x1) = N( μy+∑yx1∑x1-1(x1-μx1) , ∑y - ∑yx1∑X1-1∑x,y ) 와 같이 처음부터 x2가 없었던 것 처럼 mean과 covariance를 구할 수 있다.
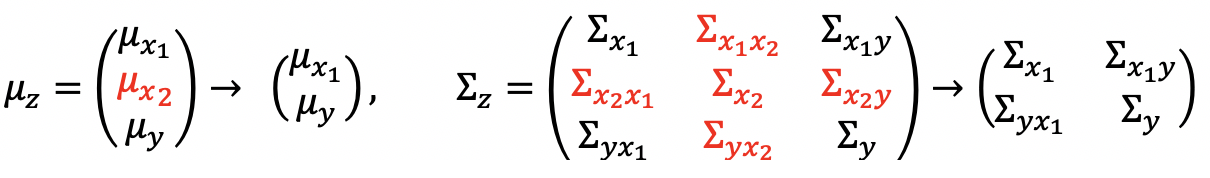
'학교수업정리 > 인공지능' 카테고리의 다른 글
| [인공지능] Graphical models (0) | 2020.11.30 |
|---|---|
| [인공지능] cover's theorem, Kernel methods (1) | 2020.11.24 |
| [인공지능] Optimization with constraint, Large margin methods (0) | 2020.10.14 |
| [인공지능] Nearest neighbor methods(이웃 알고리즘), KNN (2) | 2020.10.09 |
| [인공지능] Perceptron Convergence theorem (0) | 2020.10.06 |




